Schools Must Adopt the Science of Math
It’s Time to Bring a Research-Based Emphasis on Schema, Not Just Skills, to Every Math Classroom
The National Assessment of Educational Progress recently released the Nation’s Report Card for 2022, revealing a five-point drop in average scores for 4th grade and eight points for 5th grade—the lowest they’ve been since 2003 and 2005, respectively. Much of that slide is a result of learning disruptions caused by COVID-19, but American students weren't excelling at math before the pandemic, either. For approximately 20 years, the Programme for International Student Assessment has found American students sit, on average, in the middle of the pack when compared to their peers in other countries.
Now that the learning disruptions from the pandemic are mostly fading into the background, schools can't just return to normal to bring students back up to speed. Normal wasn't working before, and it's certainly not good enough to recover from a multi-year academic crisis.
Fortunately, researchers have a strong understanding of how people learn math, just as they did with the now widely accepted science of reading. However, that understanding is taking too long to filter into classroom instruction.
Letting Students Learn by Doing
I was a classroom mathematics teacher for many years, and I've been guilty of standing at the front of the classroom and talking too much. I assumed that if I was saying something, the students were learning it. I thought my role was to take the knowledge in my head and try to put it into theirs. I spent a lot of time asking myself, "How do we teach?"
Eventually I realized this was the wrong question. It was centered on me, the teacher, rather than the students, who were passive recipients in my model.
The more effective question is, "How do students learn?" The answer is that they don't learn by being told. They learn most effectively by doing, by grappling with tantalizingly tricky problems, trying to figure out an answer, sometimes getting it wrong, and then trying again with the new information their failure provided.
Visual math challenges are a powerful way to implement this more effective learning model at scale, and for students to learn by doing. Imagine that you have to move a character from one side of a screen to another. On the left there’s a penguin atop a stack of boxes about to be pushed from left to right. On the way there’s a pit where some of the boxes will fill in. As a student, you have to choose the height of a platform on the right onto which the penguin must walk safely.
That is a visual model of subtraction. As students try to figure out how to solve the challenge, manipulate the model, and observe the outcomes of their actions, a fascinating process called the perception-action cycle is working in their brains. All mammals use the perception-action cycle. It's how rats learn to navigate mazes and one of the key neural mechanisms that humans use to learn every day.
Building and Dismantling Schema
When humans look at a challenge like the one with the penguin and the boxes and begin thinking about how to solve it, our brains unconsciously begin firing up various schema: predicted outcomes that are already in our heads based on our prior experiences and learning. The most “powerful” schema will win out and become the prediction that we make about solving that challenge.
Once we put our prediction into action and test it as a solution, that winning schema is held in our hippocampus like a vision as we observe the results to compare against the reality we see playing out before us. If we were correct, our prediction matches reality and the hippocampus floods chemicals back along the neural pathways of that successful schema to reinforce it. This makes it bigger, stronger, more connected to other ideas and information in our brains, which basically are saying, "Wow, that works." Next time we see a similar problem, that schema will be even more powerful and likely to win out.
If we got the prediction wrong, however, the hippocampus will send different chemicals back along the unsuccessful schema, weakening it. As we see for ourselves that our prediction failed, the misconception behind it is tamped down and weakened.
Schemas and Equitable Acceleration
To help you understand what it feels like when a schema is shifted in your head, I'll share a joke. Why do people go to the mall? Take a second to think of an answer before you read on to the punchline.
Why go to one store when you can go to them all? Perhaps you groaned rather than laughing, but that feeling when the context in your head shifted from "the mall" to "them all" is a result of the fact that those two phrases are connected to different schema, sets of information and ideas.
Most jokes work like this through some kind of "schema shifting," which for some reason we respond to by laughing. But this humor also helps to reveal something crucial about how information is stored in our brains, and why the way educators typically try to help students catch up academically is not very effective.
A widely held — yet incorrect — belief has it that mathematical ideas are saved in our minds like a list, each distinct from the rest. So when an educator sees that a student is not proficient at certain grade-level skills, the typical response is to focus on those weaker skills, practicing them using worksheets or some kind of online practice program, to try and get these ideas into the student's head. But the problem isn't just that those skills are missing. The problem is that the relationships and connections between those skills are off somehow — the underlying schema is missing!
The solution, then, is to focus on building schema not skills, to help students better understand how these different ideas relate to one another. This is more effective partly because when students learn ideas as connected schema, they are learning the framework into which all the facts and skills fit, and this allows the learning to “stick.”
Without the schema, skills are learned in a shallow way, which leads to students quickly forgetting them, which is why skills-based remediation is so ineffective. Lessons that focus on building critical mathematical schema can address multiple skill deficiencies.
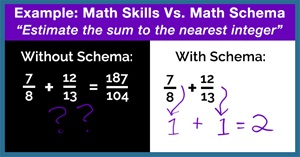
A good example of the ineffectiveness of typical skills-based instruction came to light in a question from the National Assessment of Educational Progress, which once asked students to estimate the sum of 7/8 and 12/13 to the nearest integer. Only 27% of eighth-graders and 35% of 12th-graders got the questions correct. Yet practically ALL those students would have received instruction on the skills of adding fractions with unlike denominators. This question was clearly designed to see if students understood the schema beneath it.
If they really understand what fractions are and what happens when they add them, students would see that 7/8 and 12/13 are each very close to 1 and together they would be approximately 2. If they only have the skill of adding fractions — but not the schema behind the skill — they will get 187/104, which doesn't look very much like the answer of 2. With the schema, the answer is very straightforward. Without it, the path is more complicated, disconnected from any understanding, and with lots of opportunity for error.
Every Student Can Learn This Way
All of us, children and adults alike, have innate spatial-temporal reasoning capability that is surprisingly large and trainable to high levels, and it is vastly underused in learning environments. One of the great things about this approach is that it eliminates distractions by being inherently visual. Students who don't speak the same language as their teacher can learn math and demonstrate their math knowledge with no language barriers getting in the way. Then symbols and language can be introduced later.
Research has shown how much more equitable this is for some groups of students by looking at how much they progress, relative to their current grade, from year to year as they learn math using these concepts. The Smarter Balanced Assessment Consortium's yearly assessment of 5,000 students across two grades shows that, when they used the science of math, all groups of students improved year to year — and those who were learning English and those in special ed showed by far the most growth.
It took two decades for the science of reading to move from research to the classroom. Let's not make the same mistake when it comes to implementing the science of math. Each and every struggling student deserves the best instruction we can muster, and so do all the rest.